Tartalomjegyzék

Nevezetes közepek közötti összefüggések

Nevezetes közepek közötti összefüggések

Az alábbiakban a következő állítás bizonyítását rakjuk össze több tételben: Legyen adott valahány nem negatív szám. Jelöljük mértani közepüket G-vel, számtani közepüket A-val, harmonikus közepüket H-val és négyzetes közepüket N-nel. Ekkor

H<=G<=A<=N

Egyenlőség akkor és csak akkor áll fenn, ha a számok mind egyenlőek.

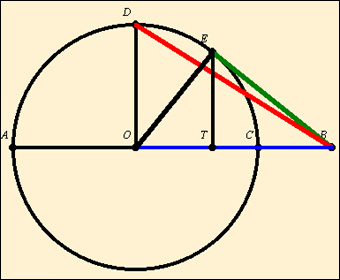
Egy szemléletes ábra:

Belátható, hogy ha AB=a és BC=b, akkor

BT az a és b harmonikus közepe
BE az a és b mértani közepe
BO az a és b számtani közepe
BD az a és b négyzetes közepe

Az ábra alapján a fenti nevezetes egyenlőtlenség jól szemléltethető.

Számtani és mértani közép közötti összefüggés

Tétel: Két nem negatív szám mértani közepe kisebb vagy egyenlő a két szám számtani közepénél, egyenlőség akkor és csak akkor áll fent, ha a két szám egyenlő.

Bizonyítás: a,b in bbR, a>=0, b>=0

(a-b)^2>=0 , egyenlőség akkor és csak akkor áll fent, ha a=b .

a^2-2ab-b^2>=0 , adjunk mindkét oldalhoz 4ab-t!

a^2+2ab+b^2>=4ab

(a+b)^2>=4ab , vonjunk gyököt mindkét oldalból!

a+b>=sqrt{4ab}=2 sqrt{ab} , osztjuk mindkét oldalt 2-vel

{a+b}/2>=sqrt{ab}

A>=G , és egyenlőség akkor és csak akkor áll fent, ha a=b .

A tétel általánosítható:

Tétel: n darab nem negatív szám mértani közepe mindig kisebb vagy egyenlő, mint a számok számtani közepe. Egyenlőség akkor és csak akkor áll fenn, ha a számok mind egyenlőek.

Bizonyítás:

a_1, a_2, ... a_n in bbR, a_i>=0 (i=1, 2, ..., n)

$G = root{n}{a_1 a_2 ... a_n}, A = {a_1+a_2+...+a_n}/n$

Első lépésben teljes indukcióval bizonyítjuk az állítást n=2^k, k in bbN esetekre.

k=1 esetet az előző tétellel már beláttuk.

Most tegyük fel, hogy n=2^k -ra már beláttuk az állítást, tehát tudjuk, hogy bármely 2^k darab nem negatív szám mértani közepe kisebb vagy egyenlő a számok számtani közepével.

Lássuk be ezt felhasználva, hogy az állítás $n=2^{k+1}$ -re is fennáll.

$G=root{2^{k+1}}{a_1 a_2 ... a_{2^{k+1}}}= sqrt{root{2^k}{a_1 ... a_{2^k}}root{2^k}{a_{2^k+1} ... a_{2^{k+1}}}}<=$ $<={root{2^k}{a_1 ... a_{2^k}}+root{2^k}{a_{2^k+1} ... a_{2^{k+1}}}}/2<= <={{a_1+...+a_{2^k}}/{2^k}+{a_{2^k+1}+...+a_{2^{k+1}}}/{2^k}}/2=$ $={a_1+...+a_{2^{k+1}}}/{2^{k+1}} =A$

Nézzük most az általános esetet. Legyen n in bbN^+ és n<2^k . A mértani közepet továbbra is jelöljük G-vel, a számtanit A-val. Ekkor:

$G=root{2^k}{G^{2^k}}=root{2^k}{G^n*G^{2^k-n}}=root{2^k}{a_1 a_2 ... a_n G^{2^k-n}}<=$

$<={a_1+...+a_n+(2^k-n)G}/{2^k}={nA+(2^k-n)G}/{2^k}$

Most szorozzuk mindkét oldalt 2^k -al

$2^{k}G<=nA+(2^k-n)G$

majd vonjunk ki mindkét oldalból (2^k-n)G -t

nG<=nA doubleright G<=A

Egyenlőség pedig csak akkor áll fent, ha a számok mind egyenlőek.

Mértani és harmonikus közép közötti összefüggés

Tétel: n darab nem negatív szám harmónikus közepe mindig kisebb vagy egyenlő a számok mértani közepénél.

Bizonyítás:

a_1, a_2, ... a_n in bbR, a_i>=0 (i=1, 2, ..., n) Jelölje továbbá G a számok mértani közepét és H a számok harmonikus közepét.

Vegyük a számok reciprokainak mértani- és számtani közepét.

$1/G=root{n}{1/{a_1}1/{a_2}...1/{a_n}}<={1/{a_1}+...+1/{a_n}}/n=1/H$

amiből mindkét oldal reciprokát véve

G>=H

A számtani és négyzetes közép közötti összefüggés

Tétel: Nem negatív számok számtani közepe mindig kisebb vagy egyenlő a számok négyzetes közepénél. Egyenlőség csak akkor áll fenn, ha a számok mind egyenlőek.

VITALAP

A számtani és mértani közötti összefüggésre egy sokkal egyszerűbb és elegánsabb Pólya György bizonyítása, kb. 3 lépésben belátható az egész. Ehhez ajánlom: http://hu.wikipedia.org/wiki/Sz%C3%A1mtani_%C3%A9s_m%C3%A9rtani_k%C3%B6z%C3%A9p_k%C3%B6z%C3%B6tti_egyenl%C5%91tlens%C3%A9g

További szép nyarat :)