Befogó tétel
Tétel: Derékszögű háromszögben a befogó mértani közép a befogó átfogóra vett merőleges vetülete és az átfogó között.
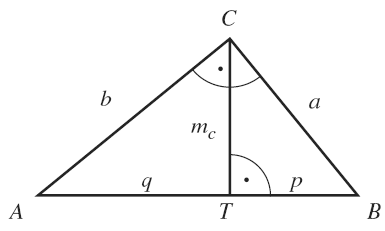
Az ábra betűjelzéseit felhasználva:
1. Bizonyítás:
A CBT háromszög hasonló az ABC háromszöghöz, mert van egy közös szögük () és egy-egy derékszögük (
, illetve
).
A két háromszögben megfelelő oldalak arányát felírva:
Ebből keresztbeszorzás után:
Kapcsolódó hivatkozások
Vita
A rajz nem megfelelő szerintem a tételhez hiszen nincs feltüntetve c, ugyanakkor vannak rajta felesleges adatok. [Coldfire]
A c oldal valóban nincs rajta, de ennek ellenére az ábra elég általános, másra is használható és szerintem egyértelmű. A tételben a betűzés mellett a csúcsokkal is ott van, hogy c = AB, így szerintem jó az ábra. [k]