Gráfelmélet

A hagyomány szerint Königsberg polgárai egy napon nehéz kérdéssel fordultak a városban lakó Leonhard Euler-hoz: mondaná már meg nekik, miért nem sikerül soha úgy végigsétálniuk a Pregel folyó hét hídján, hogy mindegyiken csak egyszer kelljenek át. (1735)

Valószínűleg ez az első gráfelméleti probléma, melynek írásos nyoma maradt, de vannak, akik Cayleynek egy 1857.-ben megjelent cikkét tekintik az első gráfelméleti tanulmánynak, melyet egy szerves-kémiai alkalmazás motivált. Olyanok is vannak, akik Guthrienek (1850. körül) De Morganhoz intézett kérdésétől számítják a gráfelmélet kezdetét. A nevezetes kérdés a négyszínsejtés korai megfogalmazása volt. Mindenesetre talán elfogadható álláspont az, hogy a gráfelmélet valahol, valamikor megszületett és az utóbbi 50 évben egyre több helyen alkalmazzák, operációkutatásban, elektromos hálózatok tervezésében, számítástechnikában.

A gráf pontokból (csúcsokból) és ezeket összekötő élekből (vonalakból) áll. Egy gráfban a pontok elhelyezkedésére, illetve az élek alakjára nem vagyunk tekintettel. A fontos csak az, hogy mely pontok vannak egymással összekötve.

A gráfot véges gráfnak nevezzük, ha a pontjainak száma véges.

A középiskolában gyakorlatilag csak véges gráfokkal foglalkozunk, így többnyire, ha mást nem mondunk, akkor véges gráfokra gondolunk.

A gráf éleit szükség esetén irányíthatjuk. Ez azt jelenti, hogy megkülönböztetjük az él két végpontját: egyiket kezdő- másikat végpontnak nevezzük.

Az irányított gráfok fogalma általánosabb, mint az irányítatlanoké, hiszen egy irányítás nélküli gráf megfeleltethető egy olyan irányított gráfnak, melyben a csúcsok megegyeznek az eredeti gráf csúcsaival, az éleket pedig két-két irányított élre cseréljük (oda-vissza a két végpont között).

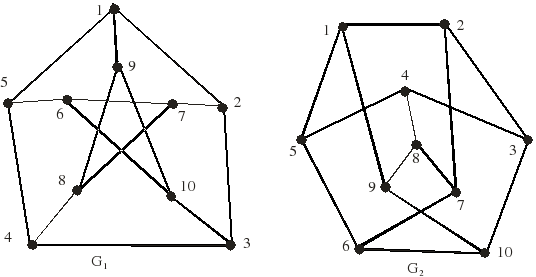Két gráf izomorf, ha pontjaik között kölcsönösen egyértelmű megfeleltetés létesíthető, és az egymásnak megfelelő pontokat a két gráfban pontosan ugyanakkor köti össze él. A pontok elhelyezkedése lehet olyan, hogy két izomorf gráf felületesen különbözőnek látszik (ld. G1 és G2 gráfokat az ábrán).

Egy gráf két pontja között futó többszörös élről akkor beszélünk, ha a két pont között több él is be van húzva, ha tehát az is fontos, hogy hányszor vannak összekötve. A többszörös élek helyett tehát használhatunk pozitív egész számokkal súlyozott éleket is.

Hurokél, melynek két végpontja azonos.

Legyen V nem üres halmaz és a V-n értelmezett homogén bináris reláció. Ekkor a G=(V,E) rendezett párt (irányított) gráfnak nevezzük, ahol V elemei a gráf csúcsai, E elemei pedig a gráf élei.

(Megjegyzés: Ez a megközelítés alapvetően irányított gráfokról szól, de nem enged meg többszörös, illetve súlyozott éleket. Amennyiben erre is szükségünk van, akkor a fenti definíiót ki kell egészítenünk egy E-n értelmezett függvénnyel - a súly függvénnyel.)

Ha a gráf nem irányított, akkor megfelel egy olyan irányított gráfnak, melyben az eredeti irányítatlan élek helyén két ellentétes irányítású él van, ami azt jelenti, hogy E - mint reláció - szimmetrikus.

Egyszerű gráfnak nevezzük az olyan gráfokat melyek élei nem irányítottak, és nincs bennük se többszörös- se hurokél.

Egyszerű gráf esetén tehát E, mint reláció szimmetrikus és irreflexiv.

A G(V,E) gráf részgráfja a G'(V',E') gráf, ha és .

Minden összefüggő gráfnak van összefüggő, körmentes részgráfja, azaz feszítőfája.

Egy csúcspont fokszáma a rá illeszkedő élek száma. Irányított gráfokban külön beszélünk be- és kifokszámról.

Ha egy csúcs fokszáma nulla, tehát az adott csúcsra nem illeszkedik él, akkor a csúcs izolált.

Állítás: Véges gráfban a fokszámok összege páros. A fokszámok összeadásakor minden élt kétszer számoltunk (a két végpontjánál) - azaz a fokszámok összege az élek számának kétszerese.

Következmény: Véges gráfban a páratlan fokú pontok száma mindig páros.

Ha a fokszám minden csúcsra azonos, a gráf reguláris. Ha ez a közös fokszám k, akkor a gráf k-adfokú reguláris vagy k-reguláris.

Azokat a gráfokat, melyekben bármely két pont között van él teljes gráfoknak nevezzük.

Az n pontú teljes gráf éleinek száma , mert egy pontból n-1 másik pontba futhat él, viszont ha ezt n pontra számítjuk, akkor minden élt kétszer számolunk, a kezdő- és végpontjánál.

Üres gráfnak nevezzük az él nélküli gráfokat.

Egy gráfban sétának nevezünk egy olyan élsorozatot, melyben az egymást követő élek közös csúcshoz csatlakoznak úgy, hogy az előbbi végpontja megegyezik az utóbbi kezdőpontjával. Fogalmazhatumk úgy is, hogy a séta csúcsoknak olyan sorozata, melyben a szomszédos csúcsok között mindig van él.

Körsétának nevezzzük az olyan sétát melynek kezdő- és végpontja megegyezik.

Az út olyan séta, melyben sem csúcs, sem él nem ismétlődik.

Ha két csúcs között van séta, akkor van út is. Ha ugyanis egy sétában egy csúcsot többször is érintettünk, akkor az első és az utolsó érintés közti körsétát kihagyva továbbra is a két pont közötti sétát kapunk, melyben a kérdéses csúcs immár csak egyszer fordul elő. Mivel az élek és csúcsok száma véges egy sétában, így a fenti „körséta elhagyás” véges sokszori alkalmazásával a sétából az összes csúcsismétlődést - és ezzel az összes él ismétlődést is - kiiktattuk, tehát egy úthoz jutottunk.

A „P és Q csúcsok között van út” kapcsolat tulajdonképpen egy a csúcsok halmazás értelmezett reláció. Ha a gráf egyszerű gráf, akkor ez a reláció egy ekvivalencia-reláció, az ekvivalencia-oszályok pedig a gráf komponensei.

• Minimális költségű út keresése

A kör olyan út, melynek kezdő- és végpontja megyegyezik.

Tétel: Ha egy véges gráfban minden pont foka legalább kettő, akkor a gráfban biztosan van kör.

Bizonyítás: Induljunk ki a gráf egy tetszőleges pontjából és haladjunk élek mentén. Ha olyan pontba jutunk, ahol még nem jártunk, akkor ebből a pontból biztosan vezet majd tovább olyan él, amit még nem használtunk, hiszen az aktuális pontba most jutottun el először, de legalább két él indul belőle. Ha olyan pontba jutunk, ahol már jártunk, akkor találtunk egy kört. Mivel a gráf véges, így előbb-utóbb (n pontú gráf esetén legkésőbb az n. lépés után) vissza kell jussunk egy korábban már érintett pontba.

minden pontja legalább fokú, akkor a gráfban van Hamilton-kör.

Egy gráf összefüggő, ha bármely két csúcsa között van út.

Állítás: G és G komplementere közül legalább az egyik összefüggő.

Bizonyítás: Tegyük fel, hogy G nem összefüggő. Legyen a gráf egy tetszőleges csúcsa P. A P-t tartalmazó komponens legyen k. G komplementerében P-ből fut él a gráf összes k-n kívüli csúcsába. Ezek közül az egyik legyen Q (k-n kívüli pont biztos van, mert G nem összefüggő). G komplementerében Q-ból fut él k összes pontjába. Így G komplementerében tetszőleges két pont - P és Q-n keresztül - legfeljebb három él hosszú úttal össze van kötve:

• Ha mindkét csúcs k-ban van, akkor mindkettő össze van kötve Q-val
• Ha mindkét csúcs k-n kívül van, akkor mindkettő össze van kötve P-vel
• Ha egyik k egy pontja, a másik k-n kívüli csúcs, akkor az első össze van kötve Q-val, Q P-vel, P pedig a k-n kívüli ponttal.

Gráf komponense a gráf egy tovább nem bővíthető (maximális), összefüggő részgráfja. Az összefüggő gráf egy komponensből áll. A komponensek száma legfeljebb a gráf csúcsainak számával lehet egyenlő - üres gráf esetén.

A komponensek lényegében a „van út P és Q között” reláció - mint ekvivalencia-reláció - által definiált ekvivalencia-osztályok által meghatározott csúcsok és a rájuk illeszkedő élek alkotta részgráfok.

A G gráf komplementere olyan gráf, melynek csúcsai megegyeznek G csúcsaival, két csúcsa között pedig pontosan akkor van él, ha G-ben nem volt.

Tétel: Egy gráf és a komplementere közül legalább az egyik összefüggő.

Bizonyítás Tegyük fel, hogy G nem összefüggő. Legyen G egyik csúcsa P, a P-t tartalmazó komponens G-ben G₁, Q pedig egy tetszőleges csúcs G₁en kívül. Ekkor G komplementerében Q-ból fut él G₁ összes pontjába, így G₁ csúcsai és Q összefüggő részgráfot alkotnak. Mivel ez bármely G₁-en kívüli pontról elmondható, így a teljes komplementer gráf összefüggő.

A fenti gondolatmenetből az is kiderül, hogy ha G nem összefüggő, akkor a komplementerében bármely két pont között kell legyen legfeljebb három él hosszú út, ugyanis:

• Ha mindkét pont G₁ csúcsa, akkor Q-n keresztül két él hosszú út van köztük.
• Ha mindkét pont G₁-en kívüli csúcs, akkor P-n keresztül két él hosszú út van köztük.
• Ha egyik csúcs G₁ csúcsa, a másik pedig kívül van G₁-en, akkor az előbbiből fut él Q-ba, Q-ból P-be, végül P-ből a G₁-en kívüli csúcsba.

A G(V,E) gráfnak szétvágó pontja , ha G-ből kihagyva v-t a rá illeszkedő élekkel együtt az összefüggő komponensek száma nő.

A G gráf kétszeresen összefüggő, ha legalább három csúcsa van és nincs szétvágó pontja.

Állítások:

1. Kétszeresen összefüggő gráfból bármely élt elhagyva a gráf összefüggő marad.
2. Kétszeresen összefüggő gráf tetszőleges két pontja között van két közös belső pont nélküli út.
3. Kétszeresen összefüggő gráf bármely három P, Q, R pontja esetén van P-Q út, mely R-t elkerüli (egyenértékű a definícióval).
4. Kétszeresen összefüggő gráf bármely három P, Q, R pontja esetén van P-Q út, mely R-re illeszkedik.
5. Kétszeresen összefüggő gráf bármely két P, Q pontja és e éle esetén van e-n átmenő P-Q út.

A G gráf csúcsainak F részhalmazát független pontrendszernek nevezzük, ha az F elemei között nem fut él.

A G gráf csúcsainak L részhalmaza lefogó pontrendszert alkot, ha G bármely élének legalább egyik végpontja eleme L-nek.

A G gráf éleinek F részhalmazát független élrendszernek nevezzük, ha az F-ben levő éleknek nincs közös végpontjuk.

A G gráf éleinek L részhalmazát lefedő élrendszernek nevezzük, ha G összes pontjára illeszkedik L legalább egy eleme.

Egy n csúcsú gráfban

• Független élek maximális száma + Lefedő élek minimális száma = n
• Független pontok maximális száma + Lefogó pontok minimális száma = n

Az olyan sétát, mely a gráf összes élét pontosan egyszer használja fel Euler-sétának nevezzük. Ha a kezdő- és végpont megegyezik, akkor Euler-körsétáról beszélünk.

Tétel: Egy összefüggő gráfban pontosan akkor van Euler-körséta, ha minden pont foka páros, illetve akkor, és csak akkor van Euler-séta, ha legfeljeb 2 (azaz 0 vagy 2) páratlan fokszámú csúcsa van.

Bizonyítás: Ha egy gráfban van Euler-körséta, akkor a körséta éleit végigmenve minden csúcsba ugyanannyiszor megyünk be, mint ki, így minden érintett pont fokszáma páros. Azokra a pontokra, melyeket nem érintettünk a körséta során, nem illyeszkedhet él, így ezek fokszáma 0. Euler-séta esetén ugyanez elmondható a séta kezdő és végpontja kivételével, így legfelejebb ezek lehetnek páratlan fokszámúak (ha nem egyeznek meg egymással).

Ha egy gráfban minden pont foka páros, akkor tudunk konstruálni, készíteni egy Euler-körsétát. Vegyünk egy tetszőleges csúcs. Erre az összefüggőség miatt nyilván illeszkedik él (kivéve azt a triviális esetet, mikor a gráf egyetlen pontból áll). Ebből a csúcsból indulva haladjunk éleken keresztül, mindig olyan új, az előzőhöz kapcsolódó élt választva, amíg ez lehetséges. A folyamat csak a kezdőpontban akadhat el, mert a séta többi pontjába mindig egy páratlanadik rá illeszkedő él felhasználásával érkezünk meg, így kell legyen még legalább egy szabad, a kérdéses pontból induló él, amin tovább haladhatunk.

Legyen egy maximális élszámú ilyen körséta K. Belátjuk, hogy K szükségképpen Euler-körséta. Ha ugyanis K nem tartalmazza a gráf összes élét, akkor kell legyen olyan él is, mely illeszkedik az eddig bejárt K körséta valamely pontjára - különben nem lenne összefüggő a gráf. Vegyünk egy ilyen pontot és ebből indulva ismételjük meg az előbbi eljárást, így kapunk egy második körsétát. Ha most a közös pontból indulva először az első, majd a második körséta élein megyünk végig, akkor a kettőt összfűzzük egy K-nál hosszabb körsétává - ami ellentmond K maximális voltának.

Ha a gráfban két páratlan fokú pont van, akkor ezeket összekötve csupa páros fokszámú pontból álló gráfhoz jutunk, melynek az előzőek miatt kell legyen Euler-köre. Ebből a körből az újonnan felvett él elhagyásával Euler-séta keletkezik.

Hamilton útnak nevezzük az olyan utat mely a gráf összes pontján pontosan egyszer halad keresztül. Ha a kezdő és végpont megegyezik akkor Hamilton körről beszélünk.

Hamilton út létezésére vannak elégséges feltételek, de a probléma általános megoldása NP-teljes, így nem remlélhető…

Néhány elégséges feltétel Hamilton-kör létezésére:

1. Ha egy n csúcsú gráfban az élek száma legalább , akkor a gráfban van Hamilton-kör
2. (Dirac tétele) Ha egy n pontú gráf

Egy gráf síkbarajzolható, ha csúcsai megfeleltethetők a sík egy-egy pontjának, élei a pontokat összekötő síkbeli, folytonos görbék, melyek nem metszik egymást. Egy síkbarajzolt gráfot röviden síkgráfnak nevezünk.

Egy síkbarajzolható gráfnak sok síkbarajzolása van, és elmondható az is, hogy van olyan síkbarajzolása is, melyben minden él egyenes szakasz.

Állítás: Egy síkgráfnak mindig van legfeljebb ötödfokú pontja.

Ha G összefüggő síkgráf éleinek számát e, csúcsainak számát cs és lapjainak számát l jelöli, akkor l+cs-e=2.

Bizonyítás: Teljes indukció az élek száma szerint.

Az nulla élű gráf egyetlen pontból áll, tehát l+cs-e=1+1-0=2

Tegyük fel, hogy a k élű, összefüggő gráfokra már tudjuk, hogy teljesül rájuk a fenti feltétel.

Vegyünk egy k+1 élű gráfot.

Ha van elsőfokú pontja, akkor hagyjuk el ezt a pontot a rá illeszkedő éllel együtt. Ezzel a pontok és az élek számát is eggyel csőkkentettük, ugyanakkor a megmaradt gráf összefüggő és csak k éle van, így erre - az indukciós feltevés szerint - l+cs-e=2. Akkor az eredeti gráfra l+(cs+1)-(e+1)=2 is teljesül.

Ha nincs elsőfokú pontja, akkor van benne kör. Hagyjuk el e kör egyik élét. Ezzel az élek számát és a lapok számát is eggyel csőkkentettük, ugyanakkor a megmaradt gráf összefüggő és csak k éle van, így erre - az indukciós feltevés szerint - l+cs-e=2. Akkor az eredeti gráfra (l+1)+cs-(e+1)=2 is teljesül.

Következmény: Mivel a konvex poliéderek csúcsai és élei síkbarajzolható gráfot alkotnak (Schlegel-diagram), így a tétel ezek csúcsaira, éleire és lapjaira is teljesül.

• Poliéderek Schlegel-diagramja
  http://geometria.sotegyak.com/math_dem/matematika/tergeometria/testek/siklaputestek/poliederek/szabtest/szabtesthtm/schlegel.htm

Egy gráf k színnel jól színezhető, ha csúcsai k osztályba sorolhatók úgy, hogy egy osztályon belül nem fut él.

Ez szemléetesen azt jelenti, hogy a csúcsok k színnel színezhetőek úgy, hogy szomszédos csúcsok mindig különböző színűek.

Bármely síkgráf jól színezhető négy színnel.

Minden síkgráf lapjai szinezhetők négy színnel úgy, hogy a szomszédos lapok ne legyenek egyszínűek.

A Négyszín tétel két alakja ekvivalens, ami a gráf duálisára való áttéréssel könnyen látható.

A G síkgráf duálisa az a D gráf melynek pontjai a G által definiált lapok, az élek a G élei, és egy él az általa határolt két G-beli lapot köti össze.