Thalész-kör

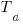
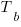
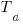
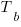
Az ABC háromszög A-ból illetve B-ből induló magasságának talppontjai illetve . Mutassuk meg, hogy a felezőmerőlegese felezi az AB oldalt.

Bizonyítsuk be, hogy a háromszög két magasságának talppontja egyenlő távol van a harmadik oldal felezőpontjától.

* Bizonyítsuk be, hogy a derékszögű gáromszög átfogója kétszer akkora, mint az átfogóhoz tartozó súlyvonal.

Mutassuk meg, hogy egy háromszög három oldalfelező pontja és az egyik magasságtalpponjta húrtrapézt vagy egyenlőszárú háromszöget határoznak meg.

* Rajzoljuk meg valamely kör AB átmérőjét, AC húrjá, és a húr meghosszabbítására mérjük fel a CD=AC szakaszt. Igazoljuk, hogy az ABD háromszög egyenlőszárú.

Egy körön kívüli P ponthoz szerkesszünk a körön olyan M pontot, amelynek P-től mért távolsága a kör átmérőjével egyenlő. Az M-en átmenő körátmérő másik végpontja N. Bizonyítsuk be, hogy a PN szakasz felezőpontja a körön van.

Írjunk kört az egyenlőszárú háromszög egyik szára mint átmérő fölé. Bizonyítsuk be, hogy ez a kör felezi a háromszög alapját.

* Szerkesszünk kört egy egyenlő oldalú háromszög magassága mint átmérő fölé. Igazoljuk, hogy a másik két oldalának a negyedrésze esik a körön kívül.

Mutassuk meg, hogy egy háromszög oldalai mint átmérők fölé szerkesztett kérék közös húregyenesei egy pontban metszik egymást.

Szerkesszünk Thalész-kört a háromszög magasságpontja és és egyik csúcsa által meghatározott szakasz fölé. Hol metszi ez a kör a háromszög két oldalát?

* Két érintkező kör egyikében egy, az érintési pontra nem illeszkedő átmérő két végpontjait kössük össze az érintési ponttal. Mutassuk meg, hogy ezek az egyenesek a másik körből egy átmérő végpontjait metszik ki.

* Kössük össze a háromszög köré írt kör középpontját az egyik csúccsal, és rajzoljunk kört az összekötő szakasz mint átmérő fölé. Bizonyítsuk be, hogy az így szerkesztett kör átmegy két oldal felezőpontján.

Két egymást metsző kör egyik közös pontjából húzzuk meg mindkettőben az átmérőt. Bizonyítsuk be, hogy az átmrők végpontjait összekötő egyenes átmegy a körök másik közös pontján.

* Egy kör valamely húrjának egyik végpontját kössük össze a kör középpontjával. Bizonyítsuk be, hogy az így kapot sugár Thalész-köre felezi a húrt.

Egy d hosszúságú szakasz két végpontja egy derékszög egy-egy szárán mozog. Mit ír le a szakasz felezőpontja?

Adott a síkon két pont, T és P. A T-re illeszkedő e egyenest forgassuk T körül, és minden helyzetébenállítsunk rá merőlegest a P pontból. Határozzuk meg az így kapott merőlegesek talppontjai által alkotott ponthalmazt.

Egy rombusz alakú keret csuklósan összeszerelt pálcákból áll. Az egyik oldalt rögzítjük. Milyen ponthalmazt alkotnak az átlók metszéspontjai, ha a többi oldalt mozgatjuk?

* Megrajzolunk egy kört, és kijelölünk egy pontot (belül vagy kívül). Adjuk meg a kijelölt ponton áthaladó húrok felezőpontjainak halmazát.

* Egy háromszögnek rögzítsük két csúcsát. A harmadik csúcs befutja a sík összes pontját. Adjuk meg az így kapott háromszögek másik két oldalegyenesén levő magasságtalppontok halmazát.

Szerkesszünk háromszöget, ha adott két magasságtalppontja és a harmadik oldal egyenese.

Adott egy egyenes és egy rá nem illeszkedő szakasz. Szerkesszünk olyan derékszögű háromszöget, amelynek derékszögű csúcsa az egyenesen van, átfogólya pedig az adott szakasz.

Tűzzünk ki két pontot, és vegyünk fel egy távolságot. Szerkesszünk két párhuzamost, melyek egy-egyx kitűzött ponton mennek át, és távolságuk akkora, mint a felvett szakasz.

Szerkesszük meg az ABC háromszöget, ha adott a BC oldal felezőpontja, a B csúcsból induló magasság talppontja, valamint a C csúcs és az M magasságpont közötti szakasz felezőpontja.

Szerkesszük meg az ABCD téglalapot, ha ismert az AB oldalegyenesének P, a BC oldalegyenesének Q, a CD oldalegyenesének R, a DA oldalegyenesének S pontja, és az AB oldal hossza.