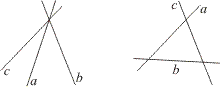Csúsztatva tükrözés
Más néven csúszástükrözés.
Tétel: Bármely három, nem feltétlenül különböző a, b, c egyenesre vonatkozó cba tükrözésszorzat (valódi vagy nem valódi) csúszástükrözés.
Bizonyítás:
Ha az egyenesek között van két azonos, úgy
- a=b esetén c(ba)=c(aa)=cI=c;
- b=c esetén cba=(cb)a=(bb)a=Ia=a;
- a=c esetében pedig, ha b* jelöli a b egyenesnek az a egyenesre vonatkozó tükörképét, úgy ba=ab*=cb*, tehát cba=c(ba)=c(cb*)=(cc)b*=Ib*=b*, vagyis a most vizsgált esetekben igaz az állítás.
A továbbiakban feltesszük, hogy az egyenesek különbözőek. Ekkor kölcsönös helyzetüket tekintve vagy
- van közöttük két párhuzamos, vagy
- páronként metszik egymást.
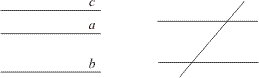
Az első esetben az egyenesek vagy egymással párhuzamosak, vagy közülük pontosan két egyenes párhuzamos (és ezeket metszi a harmadik; 8. ábra).
A második esetben a három egyenes vagy ugyanabban a pontban, vagy páronként különböző pontokban metszi egymást (9. ábra).
Először azt fogjuk igazolni, hogy ha a három egyenes egy sugársorhoz tartozik (azaz párhuzamosak, vagy egy pontra illeszkednek), akkor cba=d, ahol a d egyenest ugyanaz az eltolás (ha a és b párhuzamosak), illetve forgatás (ha a és b metszők) viszi a c egyenesbe, mint az a egyenest a b-be. E választásra ugyanis ba=cd első négy tételünk miatt, és így c(ba)=c(cd)=(cc)d=Id=d.
A még nem tárgyalt két esetet (két egyenesnek van közös pontja, ami mindhármójuknak nem pontja) egyszerre intézhetjük el.
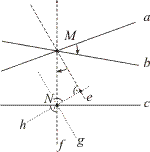
A b egyenest az a és a c egyenesek legalább egyike metszi, különben három egymással párhuzamos egyenesünk lenne. Feltehetjük, hogy az a és a b egyenesek metszik egymást, mert ellenkező esetben az egymást metsző b és c egyenesekre szorítkozva ugyanúgy bizonyítanánk, mint így. Legyen az a és b egyenesek közös pontja M, és illesszünk az M-re egy, a c egyenesre merőleges, f egyenest (10. ábra). Jelölje e azt az M ponton áthaladó egyenest , amelyet ugyanaz az M pont körüli forgatás visz az f egyenesbe, mint az a egyenest a b-be. E választásra ba=fe, vagyis (1) c(ba)=(c(fe)=(cf)e.
Jelölje N az egymásra merőleges c és f egyenesek közös pontját. Mivel a cf tükrözésszorzatot bármely két, egymást az N-ben metsző, merőleges egyenesre vonatkozó tükrözésszorzattal előállíthatjuk, ezért az ilyenek közül válasszuk meg azt a g, h párt, amelyre h⊥e teljesül. Ezzel a választással cf=hg, és (1) így alakul: (2) c(ba)=(cf)e=(hg)e=h(ge).
Az e és a g egyenesek párhuzamosak, hiszen ugyanarra az egyenesre, h-ra merőlegesek (és különböznek, mivel e az M pontra, g pedig az M-től különböző N pontra illeszkedik), azaz (2) valódi csúszástükrözés.
Forrás: A szépség matematikája (Jakucs Erika és Pogáts Ferenc - Fazekas Mihály Gyakorlóiskola)