Tartalomjegyzék
Szerkesztés
Euklidesi szerkesztés lépései
Euklideszi szerkesztésnek nevezünk minden olyan szerkesztést, ami egy darab egyélű vonalzóval és egy darab körzővel elvégezhető. Az elnevezés eredete az, hogy Euklidesz Elemek című könyvében rögzítette az általa alkalmazhatónak tartott szerkesztési eljárásokat. Ezek röviden:
- két pont összekötése egyenessel
- két egyenes metszéspontjának a megrajzolása
- kör rajzolása, ha adott a középpontja és egy pontja, vagy a sugara (két pont, melyek távolsága megegyezik a sugárral)
- kör és egyenes metszéspontjának a megrajzolása
- két kör metszéspontjának a megrajzolása
- ezek véges számú ismétlése
Alapszerkesztések
Bár az euklidesi szerkesztés lépései csak a fenti néhány eljárást engedik meg, a gyakorlatban sokszor használunk ezeből levezethető egyéb lépéseket is, ezáltal rövidebbek, átláthatóbbak lesznek a szerkesztési leírások. Ezek az úgynevezett alapszerkesztések.
Szögfelezés
Szakaszfelezés
Szögmásolás
Adott ponton át adott egyenessel párhuzamos egyenes megszerkesztése
Adott ponton át adott egyenesre merőleges egyenes megszerkesztése
A szerkesztés menete
Az egyes szerkesztési feladatokban mindig adott pontok egy bizonyos halmazából indulunk ki - ezek az alap adatok.
Az alapadatokat többféle képpen adhatja meg a feladat:
- számszerűen (pl. szerkesztendő háromszög, ha
)
- a síkban felvett pontokkal, ponthalmazokkal (adott szakasz, szög, pont…)
- ismertnek tekintendő paraméterként (pl. szerkesztendő háromszög, ha adott
)
Ez utóbbi esetben a szerkesztési feladat része (lehet) a diszkusszió, vagyis annak vizsgálata, hogy az alapadatok mely értékei esetén hány megoldása lesz a feladatnak.
Az alapadatokból kiindulva, az euklidesi szerkesztés lépéseit használva köröket, egyeneseket, esetleg szakaszokat, félegyeneseket - egyszóval vonalakat - vehetünk fel. Új ponthoz ezen vonalak metszéspontjaként juthatunk. Az új vonalak szerkesztéséhez a már megszerkesztett pontokat is felhasználhatjuk. Ilyen lépések véges során kell eljutnunk a feladatban kitűzött pontok megszerkesztéséig.
Egy pont megszerkesztéséhez tehát két rá illeszkedő vonal megszerkesztésén keresztül vezet az út. Amikor egy P pont megszerkesztésének érdekében felveszünk egy rá illeszkedő vonalat, akkor rövid úgy fogalmazhatunk, hogy „van egy vonalunk P pont számára”.
Szerkesztési tippek
Ha van két vonalunk két különböző pont számára
 Ha van két szerkeszthető vonalunk, de azok két különböző pontra illeszkednek, akkor sok esetben segíthet, ha találunk valamilyen (a már megszerkesztett pontok által meghatározott) transzformációs kapcsolatot a két pont között.
Ha van két szerkeszthető vonalunk, de azok két különböző pontra illeszkednek, akkor sok esetben segíthet, ha találunk valamilyen (a már megszerkesztett pontok által meghatározott) transzformációs kapcsolatot a két pont között.
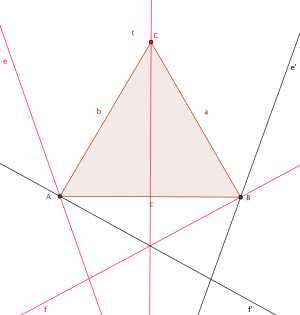
Példa: Adott egy egyenlőszárú háromszög t szimmetriatengelye, a tengelyre eső C csúcs, és egy-egy egyenes, mely illeszkedik a másik két csúcsra - e és f. Van tehát két vonalunk, e és f, de két különböző pont (A és B) számára - azaz metszéspontjuk számunkra érdektelen pontot ad.
Keressünk transzformációs kapcsolatot a két pont között! Mivel egyenlőszárú a háromszög, így A és B egymás tengelyes tükörképei a t tengelyre nézve. Ez azt jelenti, hogy ha A illeszkedik az e egyenesre, akkor A'=B illeszkedni fog az e egyenes e' tükörképére - ami szerkeszthető. Így most már van két vonalunk B pont számára (f és e'), így ezek metszéspontjaként (ha egyáltalán létezik) megkapjuk B-t.
Négyszögszerkesztések
Négyszögszerkesztésekhez általában öt adatra van szükségünk. Jó esetben ezek közül három egy háromszög három adata, mely így megszerkeszthető, majd a másik kettő adat a már megszerkesztett háromszög pontjaival újabb lépésekre ad lehetőséget.
Gond akkor van, ha semelyik három kiindulási adat nem határoz meg háromszöget. Ekkor a négyszög egy megfelelő eltolásával próbálkozhatunk…
Nevezetes szerkesztési problémák
Vannak olyan nevezetes matematikai problémák, melyek sokáig megválaszolatlanul álltak a matematikusok előtt. A szerkesztések terén is találunk ilyeneket, melyekről később algebrai eszközökkel bebizonyosodott, hogy nem oldhatók meg euklideszi szerkesztési lépésekkel:
- Szögharmadolás - Mivel a szög felezés ismert és könnyű szerkesztési feladat, azt gondolhatnánk, hogy a szögharmadolás sem lehet sokkal nehezebb.
- Kockakettőzés - Egy adott kockánál kétszer nagyobb térfogatú kocka élének megszerkesztése.
- Kör négyszögesítés - Lehet-e szerkeszteni körzővel és vonalzóval adott körhöz, vele egyenlő területű négyszöget?
Egy példa Napóleontól
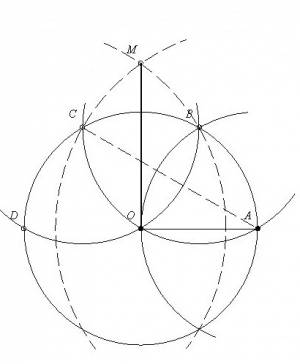
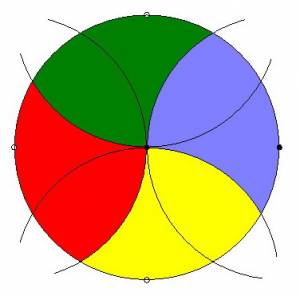
Osszunk fel egy r sugarú kört négy egyenlő területrészre! Kizárólag körzöt használhatunk!
Megoldás:
Az O középpontú kör egy tetszőleges pontjából(:=A) körívezzünk a megadott sugárral a kör kerületére,így kapjuk a B,C,D pontokat!Az AC szakasz a körbe írható szabályos háromszög oldala,ezt körzőnyílásba véve,és körözve A illetve D pontokból metszéspontként kapjuk M pontot!Pit. tétellel belátható hogy az OM szakasz a körbe írható négyzet oldala,így már könnyen oszthaó a kör négy egyenlő ívre,ahonnan már csak néhány,a megadott sugárral való körzés választ el a négy területrésztől…
A szerkeszthetőség kérdésköre
A szerkeszthetőség kérdését algebrai eszközökkel vizsgáljuk. Vegyünk fel a síkban egy derékszögű koordinátarendszert, ennek segítségével a sík pontjai és az halmaz elemei között létesíthetünk kölcsönösen egyértelmű hozzárendelést.
Definíció
Legyen . Egy
pontot H-ból euklidészi értelemben szerkeszthetőnek (a továbbiakban, ha a félreértés veszélye nem áll fönn, akkor szerkeszthetőnek, illetve körző-vonalzó pontnak) mondunk, ha létezik olyan
pontsorozat, hogy
vagy
- két kisebb indexű pontra illeszkedő egyenes metszéspontja;
- egy kisebb indexű pontokra illeszkedő egyenes és egy olyan kör metszéspontja, mely középpontja kisebb indexű pont és átmegy egy kisebb indexű ponton;
- két olyan kör metszéspontja, melyek középpontja egy-egy kisebb indexű pont és illeszkednek egy-egy kisebb indexű pontra.
Egy egyenest szerkeszthetőnek nevezünk, ha két pontja szerkeszthető . Egy kört szerkeszthető nek nevezünk, ha középpontja és egy pontja szerkeszthtő.
Definíció
Az számot körzővel-vonalzóval szerkeszthetőnek mondjuk, ha
szerkeszthető.
A következőkben az alaphalmazunk .
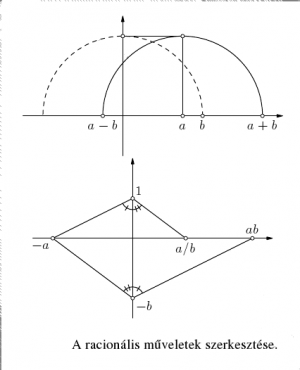 Nyilvánvaló, hogy ekkor az egész számok mind szerkeszthetőek.
Könnyen belátható, hogy szerkeszthető számokból a négy alapművelettel nyerhető számok - így tehát a racionális számok - szintén szerkeszthetőek.
Végül a magassag_tetel felhasználásával belátható, hogy bármely szerkeszthető szám négyzetgyöke is szerkeszthető.
Nyilvánvaló, hogy ekkor az egész számok mind szerkeszthetőek.
Könnyen belátható, hogy szerkeszthető számokból a négy alapművelettel nyerhető számok - így tehát a racionális számok - szintén szerkeszthetőek.
Végül a magassag_tetel felhasználásával belátható, hogy bármely szerkeszthető szám négyzetgyöke is szerkeszthető.
Az így kapott E számhalmaz test, melyben . Az ilyen testeket Euklidesi testnek nevezzük.
összes iteratív négyzetgyök bővítéseinek uniója megegyezik a {(0;0), (1;0)} halmazból euklidészi értelemben szerkeszthető pontok halmazával. Ez
a legszűkebb euklidészi számtest.
Szabályos sokszögek szerkeszthetősége
Tétel (Gauss – Wantzel)
Legyen n > 2 egész. Szabályos n szög akkor és csakis akkor szerkeszthető, ha n a következő képpen bontható prímhatványok szorzatára:
, ahol
különböző Fermat-prímek.