Legyen ABC egyenlő oldalú háromszög! Legyen továbbá x egy tetszőleges szakasz! Az ABC háromszög mindegyik oldalát hosszabbítsuk meg ezzel az x hosszúságú szakasszal, mégpedig BA-t A-n túl A'-ig, CB-t B-n túl B'-ig és AC-t C-n túl C'-ig. Bizonyítsuk be, hogy ekkor az A'B'C' háromszög köré írt kör középpontja azonos az ABC háromszög köré írt kör középpontjával. (OKTV 1987 első forduló 3. feladat)
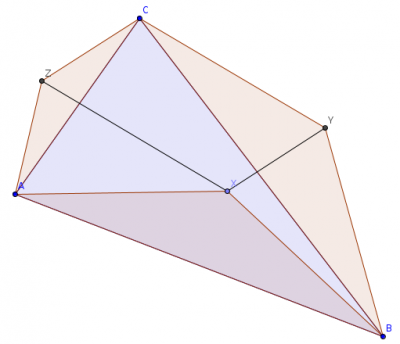
Az
ABC háromszög oldalaira szerkesszünk hasonló egyenlő szárú háromszögeket, az
ABX háromszöget befelé, a
BCY és
CAZ háromszögeket kifelé; az alappal szemközti csúcs rendre
X,
Y és
Z. Bizonyítsuk be, hogy ha az
X,
Y,
C,
Z pontok nincsenek egy egyenesen, akkor egy paralelogrammát alkotnak. (OKTV 1987 első forduló 1. példa)
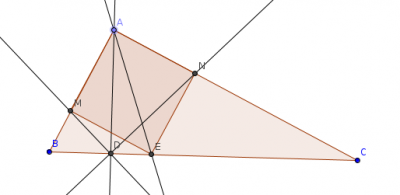
Az
ABC háromszög
BAC szöge derékszög. Az
A csúcsból húzott magasság talppontja
D, a
DAC szög szögfelezőjének talppontja
E. Jelöljük továbbá a
BDA szögfelezőjének talppontját
M-mel, az
ADC szög szögfelezőjének talppontját
N-nel. Mutassuk meg, hogy az
AMEN négyszög négyzet. (OKTV 1987 második forduló 1. feladat)
A különböző sugarú
k1 és
k2 körök az
A és
B pontokban metszik egymást. A körökön kívüli
P pontot összekötöttük
A-val és
B-vel. A
PA és
PB egyenes a köröket
C,
A,
D, illetve
E,
B,
F pontokban metszi. Bizonyítsuk be, hogy
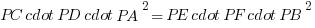
. (OKTV 1987 második forduló)
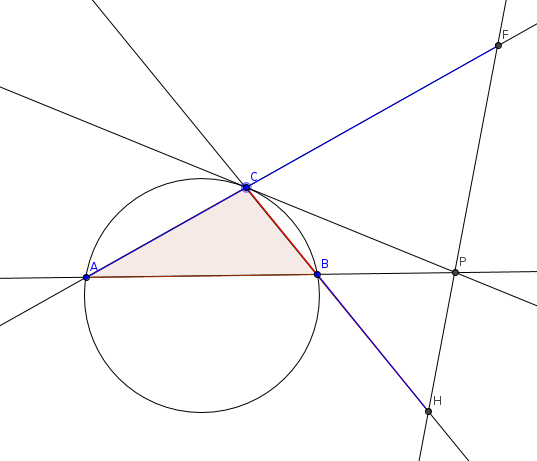
Az
ABC háromszög köré írt körhöz
C-ben húzott érintő az
AB egyenest a
P pontban metszi (
P és
B az
AC egyenesnek aznos oldalá vannak). Jelöljük
F-fel, illetve
H-val a
CPA háromszög
P-beli külső szögfelezőjének az
AC, illetve
BC egyenessel való metszéspontját. Bizonyítsuk be, hogy a
CH szakasz az
AF és
BH szakszok mértani közepe. (OKTV 1987. második forduló)
Adott az ABC háromszög. Bocsássunk merőlegest A-ból a B-beli belső szögfelező egyenesre, és B-ből az A-beli belső szögfelező egyenesre. A talppontokat jelölje D, illetve E. Bizonyítsuk be, hogy a DE egyenes a háromszög AC és BC oldalát a beírt kör érintési pontjában metszi.
Bizonyítsuk be, hogy ha egy konvex ötszög négy oldala párhuzamos a vele szemközti átlóval (pl. AB párhuzsmos CE-vel, stb.), akkor ez igaz az ötödik oldalra is. (KöMaL 1988, Gy2496)
Szerkesszük meg az ABC háromszöget, ha adott az AE súlyvonalának a hossza, valamint az ABE és az AEC háromszögek körülírt körének a sugara. (KöMaL 1988, Gy2474)
Egy húrnégyszög minden oldalára kifelé megszerkesztjük azt a téglalapot, amelynek másik oldala egyenlő a húrnégyszög szemközti oldalával. Bizonyítsuk be, hogy e négy téglalap középpontjai téglalapot határoznak meg. (KöMaL 1988, Gy2459)
Az ABCD négyszög AB és AD oldalának A-hoz közelebbi harmadolópontja K és L, a CB és CD oldalak C-hez közelebbi harmadolópontja pedig N és M. Állapítsuk meg az ABCD és a KLMN négyszögek területének arányát. (KöMaL 1988, Gy2458)
Az ABC háromszög magasságpontja M. Tudjuk, hogy AB=CM. Mekkora lehet a háromszög C csúcsnál lévő szöge? (Arany Dániel 1988, 2. forduló)


. (OKTV 1987 második forduló)
